Lecture 상태변수 피드백 제어기 예제

$G(s)= \dfrac{3s+60}{s^3+7s^2+20s+60}$이 시스템은 단위계단응답 37.5%의 오버슈트와 4.3초의 정정시간을 가진다. 이 시스템이 오버슈트가 9.48%, 정정시간 1초이하되도록 제어기를 설계하여라.

답)

1. 플랜트의 오버슈트와 정정시간을 확인 - 오버슈트 37.5%, 정정시간 4.3초
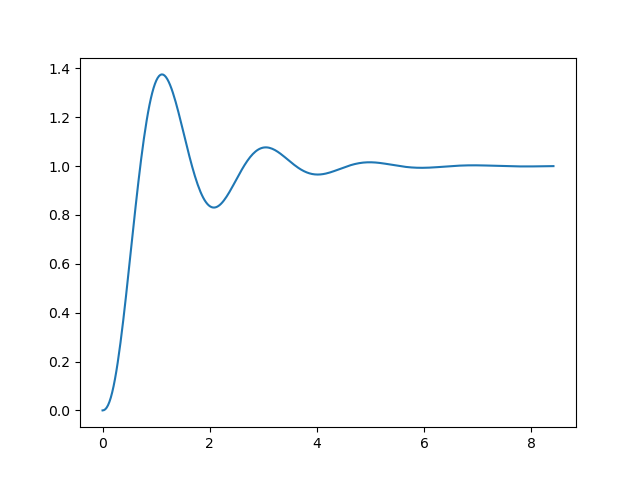
2. 오버슈트 9.48%와 정정시간 1초가 되는 시스템이 되는 $a와 \omega$을 구한다.

$$a = 0.6, \omega=5.33$$

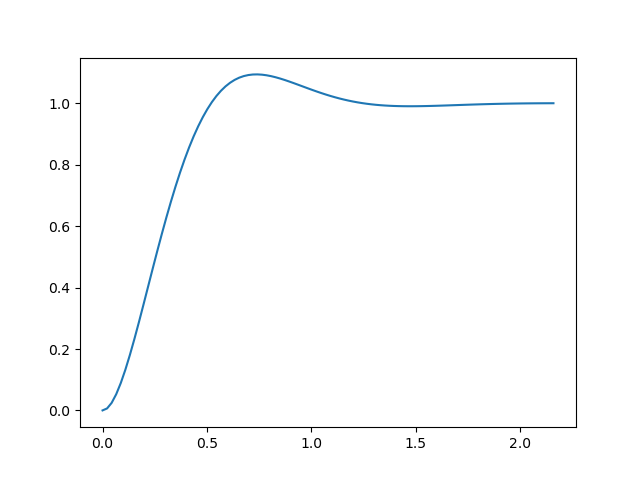
• 위 시스템의 극점 : $-3.2 \pm j4.267$

• $\alpha(s)$에 하나의 극점을 추가 -> 플랜트가 3차이기 때문임

$$\alpha(s) = (s+3.2+j4.267)(s+3.2-j4.267)(s+5*(3.2))$$

액커만 공식을 이용하여 K값을 구함 새로운 시스템은 $G_n=ct.ss(A-B*K,B,C,D)*\dfrac{\mid G \mid}{\mid G_n \mid}$

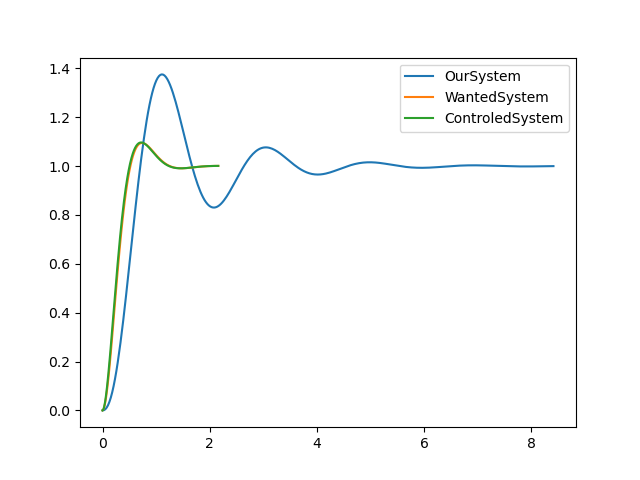
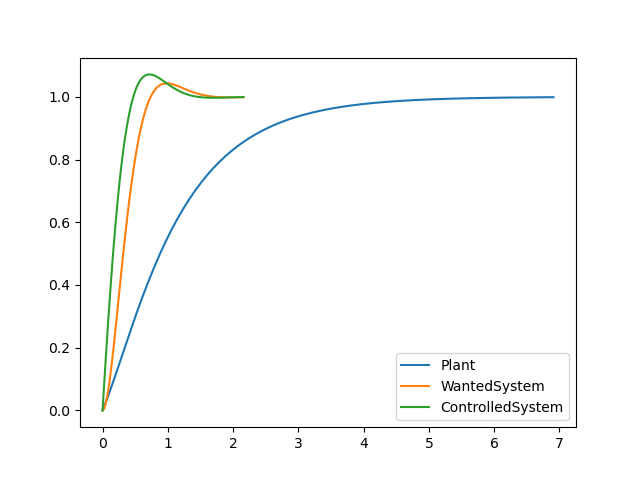
예제) 다음 시스템의 백분율 오버슈트 4.3%, 정정시간 1초가 되도록 제어기를 설계하여라.

$$\begin{bmatrix} \dot {x_1} \\ \dot{ x_2} \end{bmatrix} =\begin{bmatrix} -3&1 \\ 0&-1 \end{bmatrix} \begin{bmatrix}x_1 \\ x_2 \end{bmatrix} +\begin{bmatrix} 0 \\ 1 \end{bmatrix} u$$

$$y=\begin{bmatrix} 1.5 &0.5 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix}$$

답)

예제 9.5)

$$\begin{bmatrix} \dot {x_1} \\ \dot{ x_2} \end{bmatrix}=\begin{bmatrix} -4&-3 \\ 1&0 \end{bmatrix} \begin{bmatrix}x_1 \\ x_2 \end{bmatrix} +\begin{bmatrix} 1 \\ 0 \end{bmatrix} u$$

$$y=\begin{bmatrix} 0.5 &3 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix}$$

$s^2+8s+32$가 되도록 상태부귀환 이득벡터를 구하라.

답)

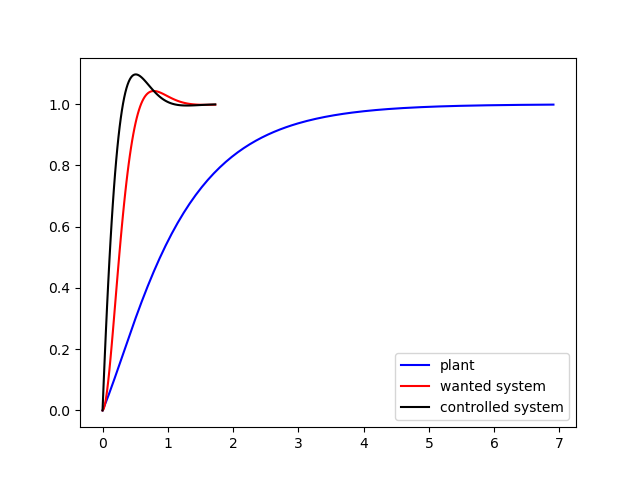
예제) 다음 시스템의 오버슈트가 10%, 정정시간 0.8초이하가 되도록 제어기를 설계하여라.

$$G(s)=\dfrac{s^2+10s+16}{s^3+10s^2+18s+16}$$