Lecture 회전자계

https://www.youtube.com/watch?v=wqrGHeuxUvI&list=LL&index=19

https://www.youtube.com/watch?v=YYQayMrK4Fo&list=LL&index=18

고정자의 자계를 회전시키는 방법은 같은 크기를 가지지만 120$^\circ$의 위상차를 가진 3상 전류가 3상 권선으로 흘러가면 일정한 크기의 회전자계를 발생시킨다.

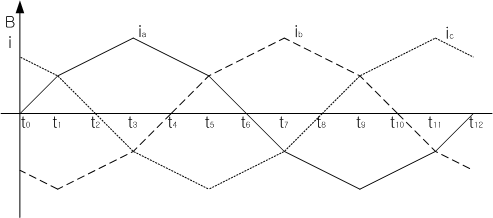
$$\begin{split} &i_{aa'}(t)=I_{m}\sin\omega t \\ &i_{bb'}(t)= I_{m}\sin(\omega t – 120^{\circ}) \\ &i_{cc'}(t)= I_{m}\sin(\omega t - 240^{\circ}) \end{split}$$

$$H \propto I \quad B =\mu H \qquad \Rightarrow B \propto I$$

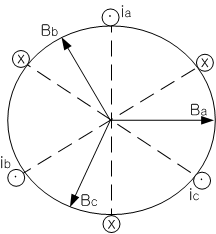
공극에서의 자속밀도는 시간과 공간의 분포에 따른다.

시간에 대한 자속밀도의 변화

$$\begin{split} &B_{aa'}(t)=B_{m}\sin\omega t \\ &B_{bb'}(t)=B_{m}\sin(\omega t –120^{\circ}) \\ &B_{cc'}(t)= B_{m}\sin(\omega t -240^{\circ}) \end{split}$$

공간에 대한 자속밀도의 변화

$$\begin{aligned} B_{ag}(t) &= B_{aa'}(t)\angle 0^{\circ} + B_{bb'}(t) \angle 120^{\circ} + B_{cc'}(t) \angle 240^{\circ} \\ &=B_{aa'}(t)(\cos 0 + j \sin 0)+B_{bb'}(t)(\cos 120 + j \sin 120) + B_{bb'}(t)(\cos 240 + j \sin 240) \\ &=B_{aa'}(t)+B_{bb'}(t)(-0.5+j\dfrac{\sqrt{3}}{2})+B_{cc'}(t)(-0.5+j(-\dfrac{\sqrt{3}}{2})) \end{aligned}$$

$$t_{0}\to\omega t = 0 \quad \Rightarrow \quad \begin{split} &B_{aa'}(t)= 0 \\ &B_{bb'}(t)=B_{m}\sin(-120)\\ &B_{cc'}(t)=B_{m}\sin(-240^{\circ}) \end{split}$$

$$\begin{align*} B_{ag}(0) &=B_{aa'}(0)+B_{bb'}(0)(-0.5+j\dfrac{\sqrt{3}}{2})+B_{cc'}(0)(-0.5+j(-\dfrac{\sqrt{3}}{2}))\\ & =0+B_{m}(-\dfrac{\sqrt{3}}{2})(-0.5+j\dfrac{\sqrt{3}}{2})+B_{m}(\dfrac{\sqrt{3}}{2})(-0.5+j(-\dfrac{\sqrt{3}}{2}))\\ & =\dfrac{\sqrt{3}}{2}B_{m}[(0.5-0.5)+j((-\dfrac{\sqrt{3}}{2})+(-\dfrac{\sqrt{3}}{2}))]\\ & =-j1.5B_{m} \end{align*}$$

$$t_{3}\to\omega t=90^{\circ} \quad \Rightarrow \quad \begin{split} &B_{aa'}(90^{\circ}/ \omega) = B_{m}\sin 90^{\circ} \\ &B_{bb'}(90^{\circ}/ \omega) = B_{m} \sin (90^{\circ} - 120^{\circ}) = B_{m} \sin (- 30^{\circ})\\ &B_{cc'}(90^{\circ}/ \omega) = B_{m} \sin (90^{\circ} - 240^{\circ})= B_{m} \sin (- 150^{\circ}) \end{split}$$

$$\begin{align*} B_{ag}(90^{\circ}/ \omega) &=B_{aa'}(90^{\circ}/ \omega)+B_{bb'}(90^{\circ}/ \omega)(-0.5+j\dfrac{\sqrt{3}}{2})+B_{cc'}(90^{\circ}/ \omega)(-0.5+j(-\dfrac{\sqrt{3}}{2}))\\ & =B_{m}+B_{m}(-\dfrac{1}{2})((-0.5)+j(\dfrac{\sqrt{3}}{2}))+B_{m}(-\dfrac{1}{2})((-0.5)+j(-\dfrac{\sqrt{3}}{2}))\\ & =B_{m}[(1+0.5(0.5)+0.5(0.5))+j(-0.5(\dfrac{\sqrt{3}}{2})+0.5(\dfrac{\sqrt{3}}{2}))]\\ & =1.5B_{m} \end{align*}$$